There is a trade-off between bias, which is the networks ability to solve the problem, and variance, which is the risk of overfitting the data. The ultimate goal is to select the model that minimizes the generalization error, which is the sum of the bias and the variance. Hence, it is necessary to estimate the generalization error to select the appropriate number of hidden units. Experimentally, this can be done with Cross Validation ( CV), Jack-knife, or Bootstrap methods [50,51]. For instance, in v-fold Cross Validation the data set is divided into v disjoint subsets, of which v-1 are used for training and one for testing. The training procedure is repeated, identically, until all subsets have been used for testing and the CV estimate of the generalization error is the average error over these v experiments
To save time one can instead of experimental methods use analytical estimates for the generalization error [52,53,54]. One approximate form for the (summed square) generalization error is [52],
where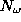 
is the number of weights in the network and 
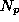is
the number
of patterns in the training set. This measure agrees well with the
experimental CV measure above [52].
However, the above methods are all a posteriori and work only in ``trial and error'' experiments where the generalization performance of different architectures are compared after training. Needless to say it is desirable to have an a priori method that selects the optimal number of hidden units before training. For classification problems, the dimension of the feature space is a rough indicator. If the network is expected to separate a closed volume in N dimensions from its exterior, the minimum number of hidden units needed is N+1. For an open volume the minimum number of hidden units is much smaller.
In function fitting problems, estimates similar to eq. (
) can
be made for certain classes of functions and networks. In ref. [36]
the following scaling relationship is given for the number of hidden
nodes that minimize the generalization error
provided that a one hidden layer MLP with linear output is used. However,
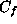is the first absolute moment of the Fourier magnitude distribution
of the function f, which is unknown! This uncertainty limits the use of
eq. () to being only a rough estimate on the number of units.
Fortunately, it is not necessary to know the exact number of hidden units beforehand. It is possible to start out with more units than needed and remove superfluous units during or after training. We discuss below how this pruning can be done.
