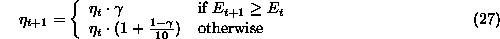
The optimal learning rate varies during learning. For BP and LV one should start out with a large learning rate and decrease it as the network converges towards the solution. Initial weight adjustments in general need to be large, since the probability of being close to the minimum is small, whereas final adjustments should be small in order for the network to settle properly. For BP and LV we use a so-called ``bold driver'' method [69] where the learning rate is increased if the error is decreasing, and decreased if the error increases:
The scale factor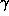 
, which is set by the parameter PARJN(11),
is close to but less than one. For MH learning we recommend an exponential
decrease of the learning rate, realized by
choosing a negative value for PARJN(11). Examples of other
more advanced methods for regulating the learning rate are found in refs.
[70,71,72].
The noise level used in LV updating should also decrease with time, preferably faster than the learning rate. We use an exponential decay governed by the scale parameter PARJN(20). This procedure is sufficient to significantly improve the learning for networks with many hidden layers [6]. From the perspective of simulated annealing and global optimization, an exponentially decreasing noise level can also be justified given that the simulation time is finite [74].
Also implemented in JETNET 3.0 are options of having the momentum and the temperature change each epoch. However, no improvements have been observed using these options.
