Introduction to the
Mean Field Method

Complex Systems Group
Department of Theoretical Physics 
Lund University
Sweden


Artificial Neural Networks (ANN), in particular feedback networks, can be used to find good approximate solutions to difficult combinatorial optimization problems. Here ANN introduces a new method that, in contrast to most existing search and heuristics techniques, is not based on exploratory search to find the optimal configuration. Rather, the neural units find their way in a fuzzy manner through an interpolating, continuous space towards good solutions. There is a close connection between feedback ANN and spin systems in statistical physics. Consequently, many mathematical tools used for dealing with spin systems can be applied to feedback ANN. Two steps are involved when using feedback ANN for combinatorial optimization:

1.  Map the problem onto an energy function, e.g.
 


 

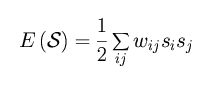
where S = {si ; i = 1 ... N} is a set of binary spin variables si = 0 or si = 1, representing the elementary choices involved in minimizing E, while the weightswij encode the costs and constraints.

2.  To find configurations with low E, iterate the mean field (MF) equations,
 


 

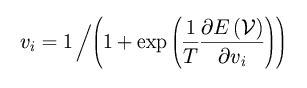
where T is a fictitious temperature. V = {vi} is a new set of variables, called the mean field variables and represents the thermal average <si>T. Each vi is a continuous variable that lies within [0,1], which allows for a probabilistic interpretation. The above, so called, mean field theory equations are solved iteratively, while lowering T.

The above equations only represent one example. More elaborate encodings have been considered, e.g. based on Potts spins allowing for more general basic decisions elements than simple binary ones. A propagator formalism based on Potts neurons has been developed for handling topological complications in e.g. routing problems.

References

Back to the Mean Field Solve home page


Last updated: Feb. 11 1998
Mail comments and queries to mattias@thep.lu.se