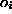 ) are analytic functions of the arguments
) are analytic functions of the arguments
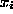 , if the activation function g is analytic. Derivatives with respect to
the inputs can therefore be computed, which simplifies error estimation.
, if the activation function g is analytic. Derivatives with respect to
the inputs can therefore be computed, which simplifies error estimation.
There are many different methods around for doing multivariate statistical analysis, function fitting or prediction tasks and ANN represents only a small subset of these. From a statistical modeling point of view, ANN models belong to the general class of non-parametric methods that do not make any assumption about the parametric form of the function they model. In this sense they are more powerful than parametric methods that try to fit reality into a specific parametric form. However, non-parametric methods like ANN contain more free parameters and hence require more training data than parametric ones in order to achieve good generalization performance [25].
Fortunately, for most HEP problems one has access to big data samples, making it possible to exploit the capabilities of non-parametric models like ANN. Tests of ANN versus standard methods on pattern recognition HEP problems are therefore in favour of ANN models [26,27,28,29,30,31]. Also, unbiased comparisons of ANN and non-ANN methods on prediction tasks are in favour of ANN [32].
Inevitably, the choice of method depends on many problem dependent factors. Is the problem complex enough to call for a non-parametric method like ANN? Is data easily available? Does the application require real-time execution? Hence, it is impossible to give a general rule on what strategy to follow (see e.g. ref. [33] for a discussion of the subject). However, ANN methods have a number of features that make them particularly attractive:
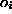 ) are analytic functions of the arguments
) are analytic functions of the arguments
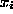 , if the activation function g is analytic. Derivatives with respect to
the inputs can therefore be computed, which simplifies error estimation.
, if the activation function g is analytic. Derivatives with respect to
the inputs can therefore be computed, which simplifies error estimation.
It is sometimes argued that statistical non-parametric methods, like decision trees etc., are preferable to ANN models since the former are easier to interpret. We disagree with this view. With the aid of a self-organizing network it is quite easy to interpret an ANN model [4].