


Next: Number of hidden
Up: Choosing the Model
Previous: ANN versus other
Classification
In classification problems, the task is to model the decision boundary
between a set of distributions in the feature space [34]. This
decision boundary is a surface of dimension N-1, where N is the number
of relevant features/inputs.
The conventional ANN algorithms for classification problems are
the MLP and Learning Vector Quantization ( LVQ) [37]. The MLP
needs 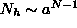 hidden units to create the decision surface,
whereas a nearest neighbour approach, like LVQ, needs
hidden units to create the decision surface,
whereas a nearest neighbour approach, like LVQ, needs 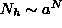 units [38]. Hence, the MLP is in general more parsimonious
in parameters than nearest neighbour approaches for pattern classification.
In special cases, when the decision surface is highly disconnected,
the LVQ approach may work better.
We have found the MLP to work better than LVQ for all HEP problems
encountered so far.
units [38]. Hence, the MLP is in general more parsimonious
in parameters than nearest neighbour approaches for pattern classification.
In special cases, when the decision surface is highly disconnected,
the LVQ approach may work better.
We have found the MLP to work better than LVQ for all HEP problems
encountered so far.
Approaches that combine the advantages of MLP and LVQ [39]
seem to work better than just using an MLP (see below on
modular architectures).
Some MLP-like approaches with skip-layer connections and iterative
construction algorithms, like the Cascade Correlation algorithm [40],
can construct very complex decision boundaries with a small number of hidden
units. It is, however, uncertain how sensitive they are to overtraining.
Function fitting and prediction
In a function fitting problem,
the task is to model a real-valued target function f from a number of
(noisy) examples.
The straightforward ANN approach is to use the MLP with appropriate
number of layers and units [41,43]. Another
is the ``local map'' where a partitioning algorithm, like k-means
clustering [44], is used to divide the feature space into
subregions. Each subregion is then associated with a function -- a
local map [42,45,46]. This method is similar
in spirit to statistical methods like regression trees and splines
[47,48]. Both the MLP and the local map approaches work
well and which method to choose depends on how local the problem is.
A third approach, which is often suggested for time-series prediction, is
to use recurrent networks with feed-back connections. However, in our
experience with time series the simple MLP produces as good solutions
as recurrent networks, within much shorter training times, given that one
is using the appropriate time lagged inputs [49].



Next: Number of hidden
Up: Choosing the Model
Previous: ANN versus other
System PRIVILEGED Account
Fri Feb 24 11:28:59 MET 1995
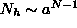 hidden units to create the decision surface,
whereas a nearest neighbour approach, like LVQ, needs
hidden units to create the decision surface,
whereas a nearest neighbour approach, like LVQ, needs 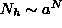 units [38]. Hence, the MLP is in general more parsimonious
in parameters than nearest neighbour approaches for pattern classification.
In special cases, when the decision surface is highly disconnected,
the LVQ approach may work better.
We have found the MLP to work better than LVQ for all HEP problems
encountered so far.
units [38]. Hence, the MLP is in general more parsimonious
in parameters than nearest neighbour approaches for pattern classification.
In special cases, when the decision surface is highly disconnected,
the LVQ approach may work better.
We have found the MLP to work better than LVQ for all HEP problems
encountered so far.