JETNET 3.0 implements the weight decay and the pruning method of
eqs. (
) and (). The Lagrange multipliers
correspond to parameters PARJN(5) and PARJN(14) respectively.
Hessian-based pruning can be done by computing the Hessian matrix,
its eigenvalues and eigenvectors: Small weights that lie inside
a flat subspace can be omitted.
Following [63], we tune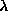 
in
eq. () according to
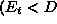or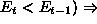 
increment 
.
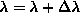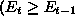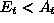and 
and
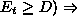decrease 
.
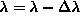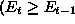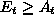and 
and
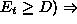rescale 
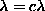, where c < 1.
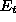is the current training error and the other
quantities are defined as
.
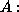
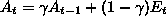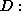
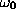in [63] is of order unity
if the activation functions for the units are of order unity. This
agrees with our experience, with the modification that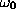 
should
follow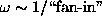 
. However, our tests were performed on problems where
the number of inputs ranged between two and ten, whereas the largest networks
in [63] have up to forty inputs. Also, on toy problems we find that
the parameter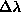 
can be increased considerable (orders of
magnitude) above the suggested default value of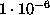 
.
In JETNET 3.0 these pruning parameters correspond to; PARJN(14) for
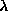, PARJN(15) for 
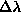, PARJN(16) for 
,
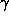PARJN(17) for c, PARJN(18) for 
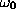, and
PARJN(19) for the desired error D. Of these, PARJN(15),
PARJN(18) and PARJN(19) are crucial.