As mentioned in Sect. 2 it is important to keep the number of weights
minimal in order to avoid overfitting. With respect to weights connecting
to sensor nodes this can be done by preprocessing. A more general approach
valid for all weights is to add a complexity term to the fitness error
(eq. (
)). The simplest such pruning procedure is
weight decay, which reads
The sum extends over all weights in the network and
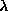is a Lagrange multiplier controlling the relative cost for
large weights. Eq. () constrains the weights to a prior
Gaussian probability distribution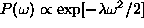 
with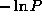 
as the complexity cost. A slightly
more sophisticated pruning option is [63]
which has zero cost for small weights and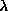 
cost for large weights.
Similar to weight decay, this corresponds to a prior weight distribution
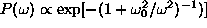. Both the weight
decay and the pruning method above are options in JETNET 3.0.
Of course, it is by no means necessary that an optimal network solution contains a set of small weights and only a few large weights. It may well be that the optimal weight distribution is multimodal, as is the case for problems with symmetries and shared weights. In ref. [57] a procedure is suggested, where the weight distribution is assumed to be a multimodal mixture of Gaussians whose means and widths are adjusted during learning. This method, which is valuable if the problem has unknown symmetries, is not implemented in JETNET 3.0.
There also exist a posteriori methods for pruning trained networks by measuring the relevance of the units [64] or by computing the Hessian matrix to remove superfluous weights [65,66]. One extremely simple method that works surprisingly well is a posteriori pruning by visual inspection: Remove all weights with a magnitude less than some threshold, provided that the inputs have been normalized.
The network must be retrained after a posteriori pruning, in order to find the global solution given the new constraints.
