


Next: The Saturation Measure
Up: Practical Implementation Issues
Previous: Computing the Hessian
JETNET 3.0 offers the possibility to use shared weights for exploiting
translational symmetries. An example is when the input units consist of a
matrix of cells, e.g. 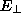 cells in a calorimeter, where it is known
a priori that identical features can occur anywhere in the matrix with
translational symmetry. It is then profitable to configure the network
so that the hidden (feature) nodes cover several overlapping smaller
portions (large enough to cover the size of a subfeature) of the input
matrix. Weights connecting to corresponding parts of the different
receptive fields are then shared, i.e. assumed to be identical.
cells in a calorimeter, where it is known
a priori that identical features can occur anywhere in the matrix with
translational symmetry. It is then profitable to configure the network
so that the hidden (feature) nodes cover several overlapping smaller
portions (large enough to cover the size of a subfeature) of the input
matrix. Weights connecting to corresponding parts of the different
receptive fields are then shared, i.e. assumed to be identical.
Such configurations can be achieved in JETNET 3.0 using the
switches MSTJN(23-27). The geometry of the input matrix
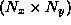 is specified with MSTJN(23) and MSTJN(24). Periodic boundary
conditions are assumed if these values are negative. The geometry of the
receptive fields
is specified with MSTJN(23) and MSTJN(24). Periodic boundary
conditions are assumed if these values are negative. The geometry of the
receptive fields 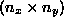 is specified with MSTJN(25) and
MSTJN(26), where
is specified with MSTJN(25) and
MSTJN(26), where 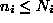 . The number of hidden units
used for
each receptive field is specified by MSTJN(27). At initialization,
an array of receptive fields is generated with maximum overlap, i.e. the
fields are only shifted one (x or y) unit at a time, and new hidden
units are generated if the specified number of hidden units is less
than necessary. Any remaining hidden units are assumed to have full
connectivity from the inputs.
. The number of hidden units
used for
each receptive field is specified by MSTJN(27). At initialization,
an array of receptive fields is generated with maximum overlap, i.e. the
fields are only shifted one (x or y) unit at a time, and new hidden
units are generated if the specified number of hidden units is less
than necessary. Any remaining hidden units are assumed to have full
connectivity from the inputs.
However, it is faster to train small network modules and later combining
them into a larger network. The above solution is inefficient for
large input matrices, since all weights are nevertheless updated.
System PRIVILEGED Account
Fri Feb 24 11:28:59 MET 1995
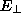 cells in a calorimeter, where it is known
a priori that identical features can occur anywhere in the matrix with
translational symmetry. It is then profitable to configure the network
so that the hidden (feature) nodes cover several overlapping smaller
portions (large enough to cover the size of a subfeature) of the input
matrix. Weights connecting to corresponding parts of the different
receptive fields are then shared, i.e. assumed to be identical.
cells in a calorimeter, where it is known
a priori that identical features can occur anywhere in the matrix with
translational symmetry. It is then profitable to configure the network
so that the hidden (feature) nodes cover several overlapping smaller
portions (large enough to cover the size of a subfeature) of the input
matrix. Weights connecting to corresponding parts of the different
receptive fields are then shared, i.e. assumed to be identical.
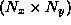 is specified with MSTJN(23) and MSTJN(24). Periodic boundary
conditions are assumed if these values are negative. The geometry of the
receptive fields
is specified with MSTJN(23) and MSTJN(24). Periodic boundary
conditions are assumed if these values are negative. The geometry of the
receptive fields 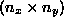 is specified with MSTJN(25) and
MSTJN(26), where
is specified with MSTJN(25) and
MSTJN(26), where 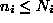 . The number of hidden units
used for
each receptive field is specified by MSTJN(27). At initialization,
an array of receptive fields is generated with maximum overlap, i.e. the
fields are only shifted one (x or y) unit at a time, and new hidden
units are generated if the specified number of hidden units is less
than necessary. Any remaining hidden units are assumed to have full
connectivity from the inputs.
. The number of hidden units
used for
each receptive field is specified by MSTJN(27). At initialization,
an array of receptive fields is generated with maximum overlap, i.e. the
fields are only shifted one (x or y) unit at a time, and new hidden
units are generated if the specified number of hidden units is less
than necessary. Any remaining hidden units are assumed to have full
connectivity from the inputs.