Minimizing eq. (
) with gradient descent is the least sophisticated
but nevertheless in many cases a sufficient method. It amounts to updating
the weights according to the back-propagation ( BP) learning rule
[5]
where
Here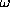 
refers to the whole vector of weights and thresholds
used in the network
.
A momentum term is often also added to stabilize the learning
where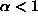 
.
Initial ``flat-spot'' problems and local minima can to a large extent be
avoided by introducing noise to the gradient descent updating rule of
eq. (). This is conveniently done by adding a properly
normalized Gaussian noise term [6]
which we refer to as Langevin updating, or by using the more crude
non-strict gradient descent procedure provided by the
Manhattan [17] updating rule
