Next: Heuristic Methods
Up: Learning in Feed-Forward
Previous: The Back-Propagation Family
Gradient descent assumes a flat metric where the learning rate 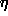 in
eq. (
in
eq. ( ) is identical in all directions in
) is identical in all directions in 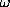 -space. This
is usually not the optimal learning rate and it is wise to modify it
according to the appropriate metric. Ideally one would like to use a
second order method like the Newton rule, that optimizes the updating
step along each direction according to
-space. This
is usually not the optimal learning rate and it is wise to modify it
according to the appropriate metric. Ideally one would like to use a
second order method like the Newton rule, that optimizes the updating
step along each direction according to

where H is the Hessian matrix
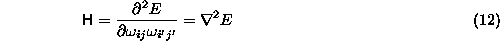
Unfortunately, computing the full Hessian for a network is too
CPU and memory consuming to be of practical use. Also, H is often
singular or ill-conditioned [18], in which case the Newton
method breaks down. One therefore has to resort to approximate
methods.
Below, we discuss those approximate methods that are implemented in
JETNET 3.0 -- an extensive review of second order methods for ANN
is found in [19].
System PRIVILEGED Account
Fri Feb 24 11:28:59 MET 1995
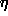 in
eq. (
in
eq. (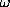 -space. This
is usually not the optimal learning rate and it is wise to modify it
according to the appropriate metric. Ideally one would like to use a
second order method like the Newton rule, that optimizes the updating
step along each direction according to
-space. This
is usually not the optimal learning rate and it is wise to modify it
according to the appropriate metric. Ideally one would like to use a
second order method like the Newton rule, that optimizes the updating
step along each direction according to