 is added to the
derivative
is added to the
derivative 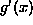 of the activation function to escape flat spots on the error surface.
In short, the updating for each weight reads
of the activation function to escape flat spots on the error surface.
In short, the updating for each weight reads
One well-known method to approximate the curvature information is
the Quickprop ( QP) algorithm [9], where the basic idea
is to estimate the weight changes by assuming a parabolic
shape for the error surface. The weight changes are then modified
by the use of heuristic rules to ensure downhill motion at all
times. Furthermore, a small constant  is added to the
derivative
is added to the
derivative 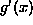 of the activation function to escape flat spots on the error surface.
In short, the updating for each weight reads
of the activation function to escape flat spots on the error surface.
In short, the updating for each weight reads
where 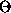 is the Heaviside step function and
is the Heaviside step function and
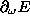 is the derivative
of E with respect to the actual weight.
This updating corresponds to a ``switched'' gradient descent with a
parabolic estimate for the momentum term. To prevent the weights
from growing too large, which indicates that QP is going wrong, a
maximum scale is set on the weight update and it is
recommended to use a weight decay term (see below).
The algorithm is also restarted if the weights grow too large
[20].
is the derivative
of E with respect to the actual weight.
This updating corresponds to a ``switched'' gradient descent with a
parabolic estimate for the momentum term. To prevent the weights
from growing too large, which indicates that QP is going wrong, a
maximum scale is set on the weight update and it is
recommended to use a weight decay term (see below).
The algorithm is also restarted if the weights grow too large
[20].
Another heuristic method, suggested by several authors
[10,21,22], is the use of individual
learning rates for each weight that are adjusted according to how ``well''
the actual weight is doing. Ideally, these
individual learning rates adjust to the curvature of the error
surface and reflect the inverse of the Hessian. In our
view, the most promising of these schemes is Rprop [10].
Rprop combines the use of individual learning rates with the Manhattan
updating rule, eq. (![]() ), adjusting the learning step for each weight
according to
), adjusting the learning step for each weight
according to
where  .
.