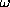A somewhat different technique to use the (approximately) correct metric,
without direct computation of the Hessian, is the method of Conjugate
Gradients ( CG), where E is iteratively minimized within separate
one-dimensional subspaces of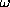 
-space (see e.g.
ref. [23]). The updating hence
reads
where the step length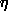 
is chosen, by employing a line search, such
that E is minimized along the direction d. The Hessian metric is
taken into account by making the minimization directions
d conjugate to each other such that
By using the negative gradient of E for the initial direction d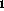
it is possible to get all the subsequent conjugate directions, without
ever actually computing the Hessian, through
where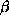 
is chosen such that eq. (
) is fulfilled.
This technique is exact if E is a quadratic form and if all the
minimizations within the subspaces are exact. However, since this is
never the case, several methods have been suggested for how to
compute the subsequent search directions. In JETNET 3.0 we have
implemented
plus a fourth one, Shanno, which is too complicated to include here. We refer the reader to [7] and [23] for a thorough discussion on these matters.
The line search part of CG minimization can be tricky and there exists a
variant, Scaled Conjugate Gradient ( SCG) [8], that avoids
the line search by estimating the minimization step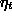 
through
where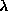 
is a fudge factor to make the denominator positive and
s is a difference approximation of H d.
This SCG method is usually faster than normal CG.
